A darts maths game and calculator

This text-based game helps you practise darts maths. Given that, it's not much of a "game". Although the maths in darts seems complicated (e.g. treble 19 added to double 17, all subtracted from 301 etc), with a surprisingly small amount of practice, it becomes fairly easy.

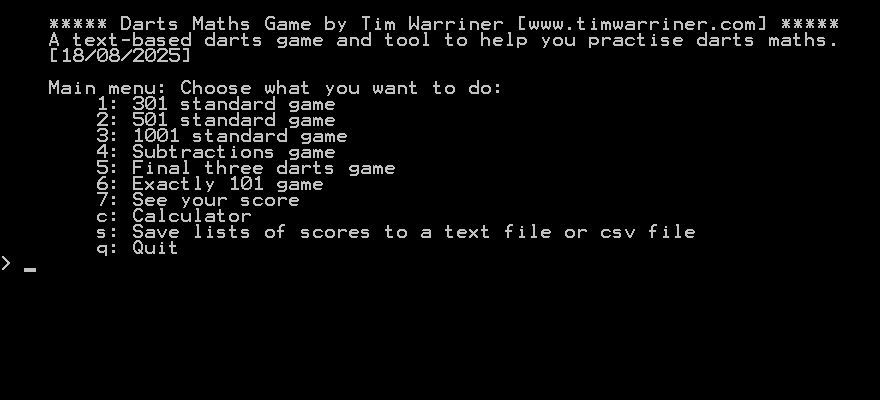
There are 6 different games to play and a calculator.

• 301 standard game: This game takes you through all the stages of a game of darts. You start with 301. You have to add up sets of three darts, then you have to subtract the result from your game total. When you reach a score that can be achieved with just three darts or fewer, you have to say which three darts you would finish on.
• 501 standard game. This is the same as the 301 game, but you start with 501.
• 1001 standard game. This is the same as the 301 game, but you start with 1001.
• Subtractions game (20 questions). You have to subtract one number from another.
• Final three darts game (20 questions). You have to say which darts would achieve a given final score while ending on a double or the bullseye.
• Exactly 101 game (20 questions). Given a number, you have to say how many points you would need to reach exactly 101. This helps improve your watching of the Star Prize round on Bullseye.
• Calculator. You type in a number between 1 and 180, and it will tell you the ways that that number can be achieved. It can also give you just the results ending in a double or bullseye.
• The program can make up text or .csv files containing all the ways to achieve different scores. For example, it can make a file containing all the ways you could achieve 60 with three darts, or even 60 with three darts ending on a double or bull. (A text file can be opened in Word, Wordpad, Notepad etc; a .csv file can be imported into Microsoft Excel.)

Download the program compiled for Windows: here.
Download the C source code: here. At the start of the source code, it explains how to compile it. You don't need any libraries that wouldn't come with a standard C compiler.

Other things

The game is entirely text based - there are no graphics.

You have to type your answers and press enter.

I have tested it a lot - it seems to work ok.

How to enter answers

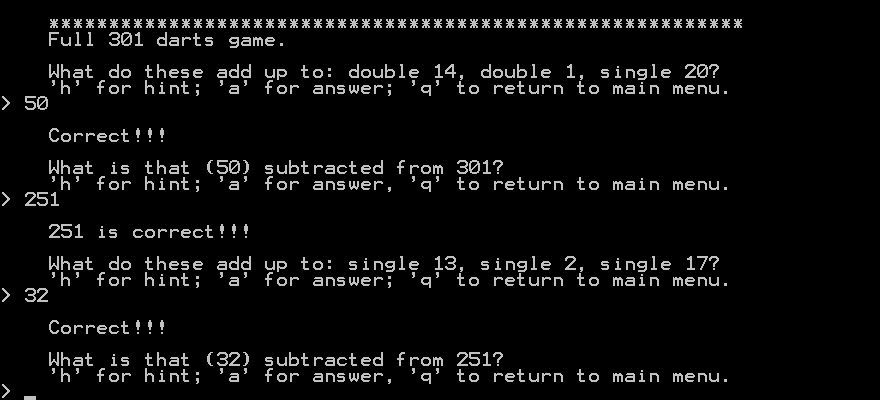
For answers that just need a number, you type the number and press enter.

For answers that need a set of darts, you can enter the answer on one line with text and numbers, but you can't use any spaces. You can type single, double, treble, bull, outerbull followed by a number if appropriate, or, more easily, you can just type the first letter of each instead:

About

The game is a text one because it's a thousand times easier than having a proper window. I wanted it to work equally well in Windows and Linux, and using text is the simplest way to do that. You can't use spaces in your answers because I was wasting too much time getting spaces to work simply, and I was more interested in the internals than the interface - the point of this thing is to help with darts maths, not to be pretty. If I were doing it just for Windows or just for Linux, I would have done things differently. You would think that entering spaces would be really easy in C, but it's more hassle than it's worth.

The hard part of writing this was finding a way to calculate which darts would produce a final score e.g. if you have 127, which darts would make that up, while ending on a double or bull. The maths involves trying to solve ax + by + cz, where a, b, c will be 1, 2 or 3; x will be from 1 to 20 (or 25 or 50); y and z will be from 0 to 20 (or 25 or 50), and whichever is the last dart thrown must be a double or bull. In the end, I found it easiest to create a table of every possible combination of three darts, and use that as a lookup table. It is essentially a rainbow table.

The next tricky thing for the 301, 501, 1001 games is how to decide when it's time to finish on a double or bull. For humans, this is really easy to calculate; for a program, it is more difficult. This program does it by preparing all the rounds in a game before any questions are asked. The program checks if the remaining score is 170 or less, and if it is, it looks it up to see if it can be achieved. If it is over 170 or if it cannot be achieved (e.g. if it's 1 or 159 etc), it alters or repeats the previous prepared round until it can. The program gets lots of goes to do this, but it usually gets a good result the second time it tries. I have tested the method literally millions of times, and it has always worked so far.

I made the 301, 501, 1001 rounds slightly biased to higher dart scores to make the game more interesting and to make it better for practising maths. There isn't much point being asked for the result of 1 + 1 + 1.

Trebles tip

If you learn that treble 19 is 57 (3 less than treble 20), treble 18 is 54 (2 x 3 = 6 less than treble 20), treble 17 is 51 (3 x 3 = 9 less than treble 20), then you will become much faster at darts maths.

Subtraction tip

Many subtractions can be made simpler in one's head with the following method. You see how far below the next hundred the lower number is, and how far above the previous hundred the higher number is, and add those together. The result of the subtraction will end in those two digits. For example:

If you have 207 - 169, then 169 is 31 below 200, while 207 is 7 above 200. The result will end in the digits 31 + 7 = 38. The actual result of the subtraction is 38.

If you have 421 - 273, then 273 is 27 below 300, while 421 is 21 above 400. The result will end in the digits 27 + 21 = 48. The actual result of the subtraction is 148.