How to calculate the highest common divisor (greatest common factor) of two numbers
[27th October, 2022]The following is a way of calculating the highest common divisor (the greatest common factor) of two numbers. I came up with this while exploring ways of calculating the discrete frequency of a sampled continuous wave. I realised that I had found two different ways of calculating discrete frequencies, with one implying that the other was a way of calculating the highest common divisor of two numbers.
In a similar way to how a songwriter might not be sure if they have written a new song or just copied one they heard earlier, I do not know if this is a new method or just a variation of an existing method. I have not seen it mentioned anywhere else, but I haven't made much of an effort to look for it. This method seems easier to use than the other methods that I have seen, but whether it is better or not is a different matter. This method requires a calculator or, preferably, a computer.
The method works with integers, and also with non-integers, for which it will give the highest common divisor that has the same number of decimal places as the number with the most decimal places.
The method:
We start with two numbers: "A" and "B". They can be both positive or both negative. They can be integers or non-integers. "A" should be greater than "B". (If the numbers are both negative, then the absolute value of "A" should be more than the absolute value of "B").We calculate this:
((A - B) / A)
... which as a picture is this:
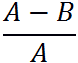
We then multiply the result of that by sequential integers from 1 upwards until the result of the multiplication is an integer.
We then divide "A" by the number by which we multiplied ((A - B) / A) to create an integer.
The result will be the highest common divisor.
Summary:
A summary of the method is:- "A" and "B" can be either both positive or both negative, and can be integers, non-integers, or one integer and one non-integer.
- "A" should be greater than "B".
- "x" is the lowest integer that if multiplied by ((A - B) / A) results in an integer.
- (A / x) is the highest common divisor of "A" and "B".
Thoughts
The biggest downside to the method is that the calculations require a computer or a calculator. It would usually be a lot of effort to do the calculations by hand.The method is very easy to program. You need to have a suitable way of detecting whether a number is an integer or not. Rounding errors can stop an integer looking like an integer.
The final step to calculate the highest common divisor involves dividing "A" by the number ("x") that when multiplied by ((A - B) / A) results in an integer. It is easy to make the mistake of dividing "A" by the resulting integer instead.
If 1 is the highest common divisor, you will end up performing as many test multiplications as the value of "A". Therefore, you can know in advance the maximum number of multiplications that you might have to perform.
Example 1:
We will find the highest common divisor of 144 and 108. "A" will be 144; "B" will be 108.We calculate ((144 - 108) / 144). It is 0.25
We then multiply 0.25 by sequential integers until the result is an integer:
0.25 * 1 = 0.25
0.25 * 2 = 0.5
0.25 * 3 = 0.75
0.25 * 4 = 1, which is an integer.
As 1 is an integer, we stop. The amount by which we multiplied our fraction to create an integer was 4. Therefore, we divide "A" (144) by 4 to find the highest common divisor:
144 / 4 = 36
Example 2:
We will find the highest common divisor of 426 and 84. "A" will be 426; "B" will be 84.We calculate: ((426 - 84) / 426) = 0.80281690 to 8 decimal places.
We then multiply that by consecutive integers until the result is an integer:
0.80281690 * 1 = 0.80281690
0.80281690 * 2 = 1.60563380
0.80281690 * 3 = 2.40845070
0.80281690 * 4 = 3.21126761
0.80281690 * 5 = 4.01408451
... and we continue until:
0.80281690 * 71 = 57, which is an integer.
Therefore, we divide "A" (426) by 71 to obtain the highest common divisor:
426 / 72 = 6
Example 3:
We will find the highest common divisor of 55.5 and 6. "A" will be 55.5 and "B" will be "6". As "A" is a one-decimal-place non-integer, the highest common divisor will be a one-decimal-place non-integer.We calculate ((55.5 - 6) / 55.5) = 0.89189189 to 8 decimal places.
We then multiply it by consecutive integers until the result is an integer:
0.89189189 * 1 = 0.89189189
0.89189189 * 2 = 1.78378378
0.89189189 * 3 = 2.67567568
0.89189189 * 4 = 3.56756757
... and so on until:
0.89189189 * 37 = 33, which is an integer.
We divide "A" (55.5) by 37 to obtain the highest common divisor that has the same number of decimal places:
55.5 / 37 = 1.5
The other methods that I have seen for calculating the highest common divisor only work with integers. You can achieve the same result with other methods by first multiplying "A" and "B" by the same power of 10 to make them both integers, and then dividing the highest common divisor by the same power of 10 afterwards. For this example, we would use 555 and 60, and the result would be 15, which we would then divide by 10.
Example 4
We will find the highest common divisor of 456 and 42. We calculate:((456 - 42) / 456) = 0.90789474 to 8 decimal places.
0.90789474 * 1 = 0.90789474
0.90789474 * 2 = 1.81578947
... and so on until:
0.90789474 * 76 = 69, which is an integer.
Therefore, the highest common divisor is 456 / 76 = 6.
We will now find the highest common divisor of 4.56 and 0.42. These are 100 times smaller than the previous numbers. We calculate ((4.56 - 0.42) / 4.56) = 0.90789474 to 8 decimal places. This is exactly the same number as for 456 and 42. This means that all the test multiplications will have exactly the same results:
0.90789474 * 1 = 0.90789474
0.90789474 * 2 = 1.81578947
... and so on until:
0.90789474 * 76 = 69, which is an integer.
As with 456 and 42, the multiplier is 76. Therefore, the highest common divisor is:
4.56 / 76 = 0.06
Example 5
We will find the highest common divisor of -363 and -44. We calculate:((-363 - -44) / -363) = 0.87878788 to 8 decimal places.
0.87878788 * 1 = 0.87878788
0.87878788 * 2 = 1.75757576
0.87878788 * 3 = 2.63636364
... and so on until:
0.87878788 * 33 = 29, which is an integer.
The highest common divisor is -363 / 33 = -11
How I discovered the method
I discovered the method when examining ways to calculate the frequencies of sampled waves. It is difficult to explain briefly, so this might not be completely clear. There are two main ideas:First, it is possible to calculate the frequency that a discrete wave will have if we know the frequency of the continuous wave that is being sampled and the sample rate. We start by calculating:
"(sample rate / frequency) * x"
... where "x" is the lowest integer that is necessary for "(sample rate / frequency) * x" to be an integer. When we have found "x", the frequency of the discrete wave will be "x" times slower than the frequency of the continuous wave.
Second, for a particular sample rate, a continuous wave will have the same samples as any continuous wave with a frequency higher or lower by an integer multiple of the sample rate. When using Fourier series analysis on a discrete wave, if we continue testing for waves after reaching the frequency equal to half the sample rate, we will find a false result that is actually the continuous wave with a frequency lower by the sample rate. The wave we find will be a negative-frequency wave (equal to the continuous wave's frequency minus the sample rate), but with the frequency made positive. The found frequency will be the sample rate minus the continuous wave's frequency. We can express this more mathematically: if the sample rate is "s" and the original continuous frequency is "f", then the negative-frequency-made-positive-frequency duplicate will have the frequency "s - f".
One interesting observation about the original continuous wave and the found negative-frequency-made-positive-frequency duplicate is that they will both have frequencies that are integer multiples of the discrete wave. Furthermore, the discrete frequency will always be the highest common divisor of both frequencies. Therefore, another way of calculating the discrete frequency is to calculate the highest common divisor of both frequencies - we calculate the highest common divisor of "f" and "s - f". We can think about this the other way around - we can calculate the highest common divisor of "f" and "s - f" by calculating the discrete frequency of the original wave using our first method. Using the same notation, the first method involved calculating:
(s / f) * x
Outside of the world of waves, if we want to find the highest common divisor of two numbers, we can say that the larger of the two numbers is "f", and the smaller is "s - f". For example, if we have the numbers 144 and 24, we can say that:
f = 144
f - s = 24
This allows us to calculate the number that, if were dealing with waves, would be the sample rate "s":
f - s = 24
144 - s = 24
-s = 24 - 144
-s = -120
s = 120
Then, we can use the first method to calculate what would be the discrete frequency if we were dealing with waves. We divide the "sample rate" (s) by the "frequency" (f), and then multiply the result by consecutive integers until the result of that is an integer.
The "sample rate" (s) divided by the "frequency" (f) is:
120 / 144 = 0.83333333 to 8 decimal places.
We multiply it by consecutive integers until the result is an integer:
0.83333333 * 1 = 0.83333333
0.83333333 * 2 = 1.66666667
0.83333333 * 3 = 2.5
0.83333333 * 4 = 3.33333333
0.83333333 * 5 = 4.16666667
0.83333333 * 6 = 5, which is an integer.
Therefore, the "discrete frequency", which is the highest common divisor, is 6 times lower than the original "frequency" (f). Therefore, it is
f / 6, which is:
144 / 6 = 24. The highest common divisor is 24.
We can change our symbols so that they no longer relate to waves. We will say that we have the two numbers "A" and "B", where "A" is the larger of the two, and that we want to find the highest common divisor. In this way, "A" is standing in for "f" and "B" is standing in for "f - s", which becomes "A - s". We calculate "s" as so:
B = A - s
s + B = A
s = A - B
Our fraction, on which we will test multiples, will be the "sample rate" divided by the "frequency". In terms of "A" and "B", it becomes:
(A - B) / A
We then multiply the fraction by increasing consecutive integers until the result is an integer. The highest common divisor will be "A" divided by the number that turned the fraction into an integer.
[Contact]