Using playing cards to store hidden data:

The implied card method for
encoding data into playing cards

Before we look at my methods of storing data in cards, we will look at more basic methods to get an understanding of their limitations.

Using the simplest method of encoding binary into playing cards, one pack of cards can represent 52 bits of data (or more if you use jokers and the instructions for playing bridge). The simplest method for encoding data is to treat a card facing upwards as a 1 and a card facing downwards as a 0. In this way, the binary number 1001 (9 in decimal) would be represented by four cards: the first and last facing upwards, and the middle two facing downwards:


This method would allow 52 bits of data to fit in one pack, but would also be fairly obvious to anyone looking for hidden data in the cards. 52 bits of data would allow for six 8-bit ASCII characters to be stored (e.g. 01000001 = "A"), or seven 7-bit ASCII characters to be stored (e.g. 1000001 = "A").


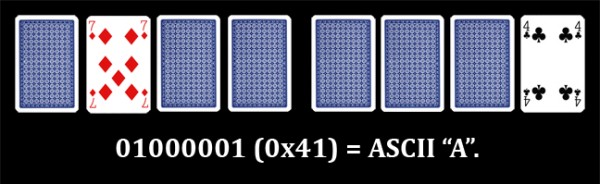
The cards could also be split into 4-bit numbers to represent reduced letter alphabet characters. For example, if we only use the 16 most popular letters of the English alphabet in our messages (etaoinsrhldcumfp), and ignore the rest (gwybvkxjqz), then 4 cards can represent one letter. The letter "e" would be 0000 (0 in decimal), "t" would be 0001 (2 in decimal), and so on. We could fit 13 letters of the alphabet into a pack in this way.

The numbers in the cards could also indicate entries in a code book. For example, 1011 could mean "send help". However, that type of code isn't relevant to what I'm trying to explain here.

Another simple method to encode data into a pack would be to mark the cards so that there was a difference between the tops and bottoms. Some packs have backs that indicate their orientation already. Those without could have one end slightly scuffed or rubbed against a candle. In this way, the cards could all be facing the same way. An upwards pointing card could be 1, while a downwards pointing card could be 0. This would allow 52 bits of data and would be less obvious than the face up/face down method. We could mark which way up the whole pack should be by how we put it into the box, or by which way up the jokers are.


These two methods could be combined to allow two completely independent strings of 52 bits of data. There can be a sequence of cards in the face up/face down method and one in the pointing upwards/pointing downwards method. The two methods could also be combined, so that each card is in 1 of 4 states: face up and pointing upwards, face up and pointing downwards, face down and pointing upwards, face down and pointing downwards. In this way, the cards are essentially indicating base 4 numbers. One card can represent one of four numbers at a time: 0, 1, 2 or 3; two cards can represent 16 base 4 numbers: 00, 01, 02, 03, 10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33; three cards can represent 64 numbers and so on. Just two cards would be needed to represent a letter in the reduced 15 letter alphabet.

Both these methods are adequate, but they cannot hold much data, and they tend to look as if they are hiding something. When combined to produce base 4 data, it is possible to hold a lot of data, but the system is incredibly cumbersome to use.

If we had circular cards with markings on the backs such as one might get on a circular protractor, the orientation of *each* card would be capable of indicating hundreds of different states. However, this method would be very difficult to use in practice.

There is much more that could be explored with face-up/face-down and orientation methods, but I will leave those for now in order to concentrate on my main idea.

The following method is fairly straightforward, the cards can all face the same way, it is far from obvious to someone who does not know how it works, it can hold more than 52 bits of data, and it lends itself perfectly to one-time pad encryption.

Previous page    Next page