Using playing cards to store hidden data:

The implied card method for
encoding data into playing cards

Recursive Implied Card Method

The Implied Card Method as described so far is straightforward and fairly efficient. However, it is possible to take it to an even higher level that allows us to encode even more data into a pack of 52 cards. This adds more complexity to the idea, which will make decoding the pack more time consuming. Encoding the pack, however, is not much different to before.

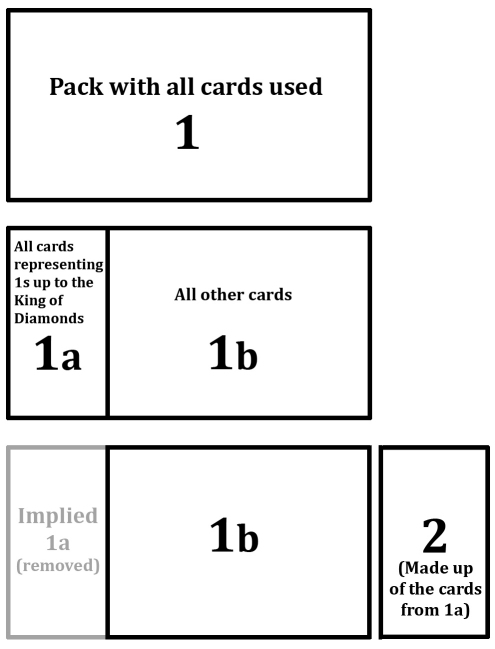
This optimisation is based on the following idea when thinking about an already encoded pack of cards: If we were to remove the part of the encoded pack up to where the previously absent cards started re-appearing (i.e. up to and including the king of diamonds, or at least where the king of diamonds should appear), we would still have enough information in the rest of the pack to work out what the first section would have been. The contents and order of the first part of the pack are logically implied by the existence of the cards in the second part of the pack. Therefore, we do not actually need the first part of the pack to be included in our pack of cards for it to be successfully decoded, and therefore, we can use all those cards again to represent even more numbers.

For example, if there is an ace of spades anywhere in the second part of the pack, then we know for sure that it was an absent card in the first part of the encoding, and that it does not appear in the first part of the pack. Similarly, if there is not an ace of spades anywhere in the second part of the pack, we know for sure that it was present in the first part of the encoding. If the ace of spades was in the first part of the pack, it would have been the very first card - there is nowhere else it could have been. Similarly, for example, if the king of diamonds was in the first part of the pack, it would have been the last card - there is nowhere else it could have been either. In this way, any card that is not in the second part of the pack must have been in the first part of the pack, in a position that we know.

Whereas before, we have been reusing cards that represented 0s, now we will be reusing cards that originally represented 1s. Before now, our cards were reused by just putting them at the back of the pack. Now we have to make sure that we keep them separate from the rest of the pack. It is vital not to confuse our two parts of the pack or else the second part will be decoded incorrectly. To do this, we can separate them with a joker or the "rules for bridge" card.

When encoding a pack that will eventually have a reused section, we encode normally for the whole of the pack until we have run out of cards in exactly the same way as normal. We then split the encoded pack at the point where the king of diamonds first appears (or where it should first appear). The first part we will call "Part 1a"; the second part, "Part 1b". We then put a Joker on the back of "Part 1b" (the back of the entire pack) to act as a separator, and encode the rest of our numbers into "Part 1a" as if nothing were different. After the encoding, to indicate that "Part 1a" now contains a different combination of the same cards, we will call it "Part 2".


When it comes to decoding a pack with a reused section, we are missing "Part 1a" so we have to analyse "Part 1b" to see which cards would have been in "Part 1a". In other words, we just see which cards are in "Part 1b", and mark them as 0s in our first Decoding Row (made up as usual to be a list of all 52 cards in order from the ace of spades to the king of diamonds). We mark them with 0s because if they are in "Part 1b", they could not have been in "Part 1a". (We cannot analyse "Part 2" to do this as "Part 1b" might contain a few final unused cards from the first encoding). When we have marked the 0s, we then mark the other entries with 1s. Having done that means that the Decoding Row shows how "Part 1a" originally looked. We then decode "Part 1b" as normal in a new row underneath, based on the cards marked with 0s in the first row. We go through "Part 1b" as normal, marking 1s for present cards and 0s for absent cards, and making new rows underneath when needed.

When it comes to "Part 2", we know the original order of those cards and which ones were actually there, as they are the cards marked with 1s in the first Decoding Row. Therefore, we can create a new set of Decoding Rows on a separate piece of paper starting with a row listing those cards. We then decode "Part 2" using that row as normal, creating more rows as needed. Our final binary number will be based on both sets of rows.

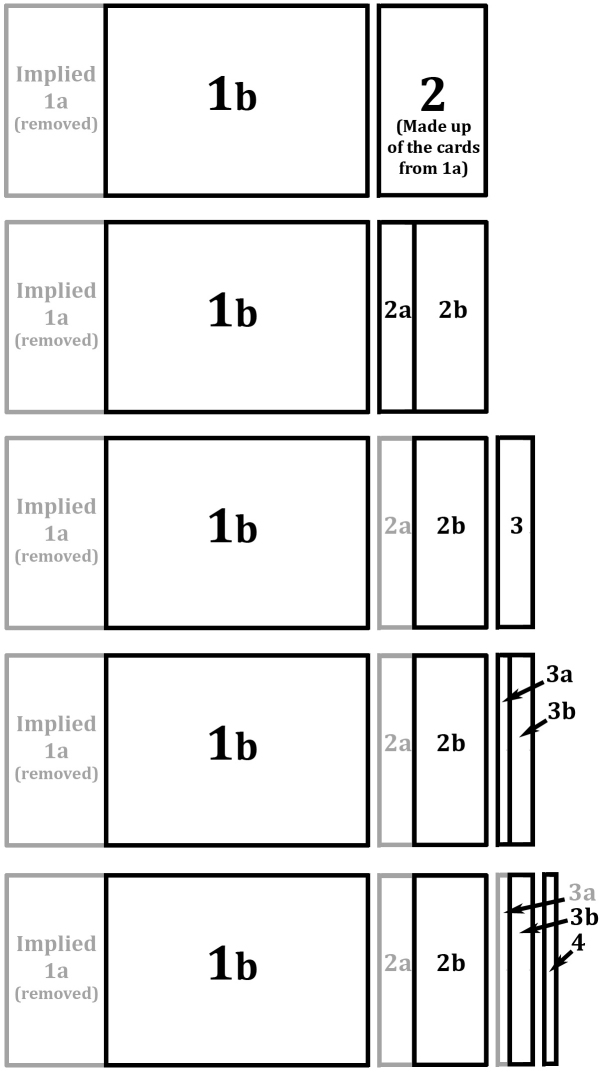
As I have just said, we know which cards are in "Part 2" from examining the cards in "Part 1b". We also can tell which cards are in the first part of "Part 2" from the cards in the second part of "Part 2". We do not actually need the first part of "Part 2" to be kept in the pack to decode everything properly. Therefore, we can split "Part 2" and turn the beginning of it into a new part, "Part 3". We can encode cards into "Part 3", and then that can, itself, be split to produce a part that can, in turn, be split and so on. In this way, we can carry on using smaller and smaller parts derived from previous parts until we get to one with too few cards to use. We would need to keep putting dividers into the pack to indicate where the parts are separated, and after every level of splitting, decoding would become slightly more complicated. The ability to keep reusing smaller and smaller portions of the pack is why I call this the Recursive Implied Card Method.

Here is a diagram showing how we split the pack for more "recursions":




To show how much more we can encode using this optimisation, and to help explain it, I will use the original example of encoding the binary numbers from 0001 to 1111, and then from 0000 to 1010. We will continue from where we stopped in that example. In that case, we ended up with three leftover cards: the 4 of hearts, the 5 of spades and the 6 of clubs. Although it would be useful to use them again, we have to keep them at the end of the pack where we had them, as, despite not representing any cards, they are needed to indicate which cards are in the first part of the pack. These extra cards will not confuse matters if the person decoding the pack is aware that they are decoding 4-bit numbers. Three cards on their own that do not make up a 4-bit number will be interpreted as the leftover, meaningless cards that they are.

To see where we need to split the pack, we look through it until we find the place where the king of diamonds either is or should be. The cards up to and including the king of diamonds (if it is there) will make up "Part 1a". [The splitting point will also be the position of the last card that represented a 1 before the cards started to be reused. This is also the point just before we started reusing cards that had previously been zeroes. Putting this yet another way, this is the point at which, were we decoding the cards, we would have finished our first Decoding Row. Usually (but I do not think necessarily always) this will be the first point where the cards of the pack stop being in order.] In our example, the king of diamonds is there, and the next card is the ace of spades. The ace of spades is the first of the cards that were used to represent a zero on their first appearance, so that is where we will split the pack. Our cards from the start (the 4 of spades) to the king of diamonds inclusive will make up our "Part 1a" (and the basis of our future "Part 2"). The other cards will make up "Part 1b". There are 25 cards in "Part 1a" and 27 cards in "Part 1b".


We put "Part 1b" face down on a table, and put a joker face down on that. The joker will indicate the point where the new third section ("Part 2") will begin, and it is also an indicator that we are using the Recursive Method.

We then take "Part 1a" in one hand and start encoding numbers into it in the usual way. We will put the kept cards (the ones that represent 1s) face down on the existing pile on the table, and pass the removed cards (those that represent 0s) to the back of "Part 1a" to be used again in the future.

Our first number is 1011. The top cards of the ones we have in hand are the 4, 7, jack and queen of spades. We put the 7 at the back, and put the other three cards face down on our pile on the table.

Our next number is 1100. The top cards are the ace, 5, 7 and 9 of clubs. We keep the ace and the 5, and we put them on our pile. We remove the 7 and the 9, and we put them to the back.

The next number is 1101. The top cards are the 10 and king of clubs, and the ace and 2 of hearts. All except for the ace of hearts go on the pile.

We continue like this until we reach 1111, at which point, we will keep the king of hearts, and the 2, 4 and 5 of diamonds. Then, we can start at 0000 again. The cards are the 6, 7, 10, and jack of diamonds. We pass them all to the back. We then continue until we have run out of cards. The last number we can do is 0101. After that, we have three cards left: the 7 and 10 of diamonds, and the 7 of clubs. We cannot use these cards, so we put them face down on the table pile and we are done. The pack now consists of "Part 1b" and "Part 2". "Part 1a" no longer exists.

We now have a pack of cards that has the numbers 0001 to 1111 (1 to 15 in decimal), 0000 to 1111 (0 to 15 in decimal) and 0000 to 0101 (0 to 5 in decimal) encoded in it. Therefore, it contains 37 4-bit numbers, which amounts to 148 bits of data. Before our new Recursive Method, we could only store 26 numbers, which amounted to 104 bits of data.




Decoding will take up more time than before. The person decoding needs to be sure that we are using the Recursive Method. This can be discovered by the presence of a joker in the middle of the pack. Without knowing that we are using the Recursive Method, someone might start decoding the pack as normal, in which case, they would just produce meaningless data.

First, we split the pack into two parts: the part before the joker and the part after the joker. The part before the joker is "Part 1b", the part after the joker is "Part 2". We put "Part 2" and the joker in a safe place for later.

We write out a Decoding Row as we would do normally. It will contain all the possible cards in a pack in order, from the ace of spades to the king of diamonds for each suit.

Step 1: We need to recreate the contents and layout of the missing "Part 1a". To do this, we look through "Part 1b". If a card in our Decoding Row appears in "Part 1b", we put a 0 underneath its entry. We put a 0 against the entry because if a card is in "Part 1b", it could not have been in "Part 1a". When we have been through "Part 1b", we mark 1s under the other cards in the row. [We know that if a card is not in "Part 1b", then it must have originally been in "Part 1a".]

In our example, the ace of spades is in "Part 1b", so we put a zero against it in our row. The 2 and 3 of spades are similarly in "Part 1b", so they get zeroes too, and so on.

[A picture of the process of going through the cards in "Part 1b" one by one to create the original order and contents of "Part 1a":]


Doing the above process not only recreates the decoded numbers from "Part 1a", but it also shows us the original order of the cards we will find in "Part 2" for when we come to decode that.


Step 2: Now we decode "Part 1b" in the usual way, as if it were a continuation of that row (which it technically is). We write out a new row underneath the first row, made up of the cards that were marked with 0s in that row. In our example, it will contain the ace, 2, 3, 5, 6, 8, 9, 10, and king of spades; the 2, 3, 4, 6, 8, jack, and queen of clubs; the 4, 5, 6, 8, 9 and queen of hearts; the ace, 3, 8, 9, and queen of diamonds.

Next, we go through "Part 1b" - marking 1s against cards that are there and 0s against cards that are absent. When we get to the end of the row, we create a new row underneath consisting of the cards marked with 0s in the previous row. We carry on marking 1s and 0s, and creating new rows until the whole of "Part 1b" is done. We will end up using 6 Decoding Rows, the last of which contains two cards: the 5 of spades and the 6 of clubs. The set of completed rows should be identical to those when we first counted up from 0001 to 1111 and from 0000 to 1010 in the example in the Basic Encoding explanation.


Step 3: Now we decode "Part 2". To do this, we create a new row on a separate piece of paper, listing just the cards that were marked with 1s in the row when we decoded the implied "Part 1a". In this example, this new row will consist of: The 4, 7, jack and queen of spades; the ace, 5, 7, 9, 10 and king of clubs; the ace, 2, 3, 7, 10, jack and king of hearts; the 2, 4, 5, 6, 7, 10, jack and king of diamonds.

We then go through "Part 2", decoding it in the normal way - marking off the cards that are present with 1s, and the cards that are absent with 0s, and creating new rows when we get to the ends of old rows. In this example, we will use 5 Decoding Rows, the last of which has just one card in it: the 7 of clubs.

After doing that, we have completely decoded the cards for the whole pack. We can read the binary numbers from the set of rows for "Part 1a" and "Part 1b", and from the set of rows for "Part 2".




Now we have seen how the recursive method works in the example, we can apply it again to the pack and use the first part of "Part 2" to encode more cards. We will leave "Part 1b" as it was.

First, we find the point where we will split the pack. We will search from the start of "Part 2" until we reach the point where the cards started to be reused. The most certain way of knowing this point is to have made a note of it when the pack was being encoded. [Another way that has always worked so far for me, but might not always work, is to look for the first place where the cards stop being in order. I think there may be situations where this is not reliable, but I have not given it much thought.] If you have checked to see if your encoding was correct so far by decoding it as you went along, and you kept the Decoding Rows, then the point where you split "Part 2" will be at the last card that was marked with a 1 in the first row for "Part 2".

In this example, we split the pack after the 5 of diamonds. Our "Part 2a" will consist of: the 4, jack and queen of spades; the ace, 5, 10 and king of clubs; the 2, 3, 7, 10 and king of hearts; and the 2, 4, and 5 of diamonds. Our "Part 2b" will be the 9 of clubs onwards.

With "Part 1b" face down on a table, we put a joker over it to act as a marker. We then put "Part 2b" face down on top of that, and another joker on top of that.

Using "Part 2a", we will now carry on counting from where we left off. We will put "kept" cards face down on the rest of the pack; we will pass "removed" cards to the back of "Part 2a" (which will become Part 3 when we are done).

Our first number to encode will be 0110. The first four cards available are the 4, jack and queen of spades, and the ace of clubs. We keep the jack and queen, and we pass the 4 and ace to the back of "Part 2a". The encoding for the rest of "Part 2a" is as normal. The last number we can encode is 1011. We are left with two cards: the 10 of hearts and the 4 of diamonds. We have encoded six new 4-bit numbers into this section. Therefore, we have 43 4-bit numbers (172 bits of data) encoded in this pack of 52 cards.




Because this example is now getting more complicated, I will show how to decode this pack from the very beginning.

Looking through the cards, we can see two jokers which means that the pack has 3 distinct existing parts: "Part 1b", "Part 2b" and "Part 3". It has 5 parts in all:
- "Part 1a" (which is not actually there, but can be worked out from "Part 1b")
- "Part 1b"
- "Part 2a" (which is not actually there, but can be worked out from "Part 2b"
- "Part 2b"
- "Part 3"

"Part 3" was originally made up from "Part 2a", and "Part 2a" was in turn made up from a portion of "Part 2", which in turn was originally "Part 1a".

Step 1: First, we need to recreate the non-existent "Part 1a". Therefore, we need to find which cards would have been in it and where they were. To do this, we write out a Decoding Row of all 52 cards in the pack in order, from the ace of spades to the king of diamonds for each suit. We will call this "Row A". Next, we look through the cards in "Part 1b", and put zeroes under every row entry for each card that appears in "Part 1b". If a card is in "Part 1b", it means it was not in "Part 1a". When we have been through the row, we put 1s underneath the entries that do not have 0s underneath them.

Step 2: Next, we decode "Part 1b". This is decoded normally as if it were an extension of "Part 1a". In other words, we write out a second row underneath "Row A" containing the cards that were marked with zeroes in "Row A". We then go through "Part 1b" and mark 1s for existing cards, and 0s for absent cards as normal. We create more rows if needed until we have completed "Part 1b".

Step 3: Next, we need to recreate the non-existent "Part 2a". We can do this by finding out which cards were in the whole of "Part 2" before it was split, and which cards are currently in "Part 2b". The cards that appeared in the whole of "Part 2" before it was split are those marked by 1s in "Row A". Therefore, we create a new row based on those cards on a separate piece of paper, and we will call the new row, "Row B". "Row B" will consist of: the 4, 7, jack, and queen of spades; the ace, 5, 7, 9, 10 and king of clubs; the ace, 2, 3, 7, 10, jack and king of hearts; and the 2, 4, 5, 6, 7, 10, jack and king of diamonds.

To see which cards were actually in "Part 2a", we look through the cards in "Part 2b". When a card in "Row B" appears in "Part 2b", we mark it with a zero (because if it is in "Part 2b" then it was not in "Part 2a"). When we have been through the row, we put ones under the cards without zeroes.

Step 4: We then decode "Part 2b". This is decoded normally as if it were an extension of "Part 2a". We write a row underneath "Row B" of the cards that were marked with 0s in "Row B". We then go through "Part 2b" as normal, marking cards that are present with 1s and those that are absent with 0s, and making new rows as needed. In this example, four rows are needed to decode "Part 2b", which added to the first row (Row B) makes 5 rows needed to decode both "Part 2a" and "Part 2b". The last row has only one card in it: the 7 of clubs.

Step 5: On a separate piece of paper, we then create a list of all the cards marked with 1s in the top row of "Row B". We will call this list, "Row C". In this example, "Row C" will contain the cards: the 4, jack and queen of spades; the ace, 5, 10 and king of clubs; the 2, 3, 7, 10 and king of hearts; and the 2, 4 and 5 of diamonds.

We decode "Part 3" of the pack normally using "Row C". Cards that are absent are marked with 0s; those that are present are marked with 1s. We finish this row and create new rows underneath until we finish "Part 3". We end up using 3 rows to decode "Part 3". The last one contains 3 cards: the 5 of clubs, the 10 of hearts and the 4 of diamonds.

When that is done, we have successfully finished decoding the pack. We can read off our original number by reading the 0s and 1s of "Row A" and the rows underneath it, "Row B" and the rows underneath that, and "Row C" and the rows underneath that.




1: Encode the whole pack as normal.
2: Split the pack at the point where cards that represented 0s came around the second time. We now have two parts: 1a and 1b.
3: Encode numbers into "Part 1a" and put it (now referred to as "Part 2") to the back of "Part 1b" separated by a joker.

Then repeat the following forever:
4: Split "Part X" at the point where cards that represented 0s came around the second time in it, creating "Part Xa" and "Part Xb".
5: Encode numbers into "Part Xa" and put it (now referred to as "Part X+1") to the back of "Part Xb" separated by a joker, the rules for bridge, or a piece of paper.




1: Make a list of all 52 cards in the pack in order from the ace of spades to the king of diamonds for each suit in a row across the top of a piece of paper. We will call this, "Row A".

2: If "Part 1" is *not* split with a joker, we go through the pack as normal starting with "Row A", and we are done.

3: If "Part 1" *is* split with a joker, we recreate "Part 1a" by marking 0s against the cards in "Row A" that appear in "Part 1b", and 1s against the cards that do not. We then carry on decoding "Part 1b" as normal as if it were a continuation of "Part 1a".

4: We create a list of all the cards marked with 1s in "Row A" on a separate piece of paper. We call this, "Row B".

5: If "Part 2" is *not* split with a joker, we go through it as normal using "Row B", and we are done.

6: If "Part 2" *is* split, we recreate "Part 2a" by marking 0s against the cards in "Row B" that appear "Part 2b", and 1s against the cards that do not. We then carry on decoding "Part 2b" as normal as if it were a continuation of "Part 2a".

7: We create a list of all the cards marked with 1s in "Row B" on a separate piece of paper. We call this, "Row C".

8: If "Part 3" is *not* split, we go through it as normal using "Row C", and we are done.

9: If "Part 3" *is* split, we recreate "Part 3a" by marking 0s against the cards in "Row C" that appear in "Part 3b", and 1s against the cards that do not. We then carry on decoding "Part 3b" as normal as if it were a continuation of "Part 3a".

10: We create a list of all the cards marked with 1s in "Row C". We call this, "Row D".

11: If "Part 4" is *not* split, we go through it as normal using "Row D", and we are done.

12: If "Part 4" *is* split... etc etc etc.

And so on....




Just for the sake of showing the method being used to encode numbers seen "in the wild", here are some examples:


MD5 Hash:

The MD5 hash of the word "apple" is 1f3870be274f6c49b3e31a0c6728957f.

This is 00011111, 00111000, 01110000 etc in binary, when it is 128 bits long. On the first (non-recursive run), we can encode 96 bits, which (in hex) is: "1f3870be274f6c49b3e31a0c". We have four cards left over.

"Part 1a" (= "Part 2") has 28 cards in it, and we can encode the rest of the number easily into it without needing to split "Part 2" afterwards. We have 10 unused cards left over. On decoding, those 10 unused cards will all appear as 1s, but because we know the length of the binary number (128 bits), that will not be a problem. If we did not know the length, then we might presume that the last numbers were 11111111, 11111111 (0xff in hex), followed by 2 single 1 bits.


A long string of hex bytes:

Here is an old public key for the certificate for the google.com website. There is no relevance to this number or any use in encoding it - it is just a long number that I found on the internet. The key is as follows:
"04 f2 e1 38 24 4a 53 3d a8 0d 9b 34 7c 71 26 29 84 38 51 5a 2d ca 00 7b cb 1b 38 0c fa 93 f2 c6 b7 ba 08 f4 21 c0 b5 28 9e 19 66 a3 45 7d 70 63 18 12 a1 0f 52 7e 29 ef ec 36 2b 06 29 cc 26 f1 96"

In binary, this starts as: 00000100, 11110010, 11100001 and so on.

On the first run before recursion, we can encode 104 bits, and we have 6 cards left over. On the first recursion run (i.e. after creating "Part 2"), we encode another 44 bits and have 5 cards left over. On the second recursion run (i.e. after creating "Part 3"), we encode another 8 bits and have 5 cards left over. We only have 3 cards available for "Part 4" which is not enough to encode anything, so we have to stop there.

Therefore, in total we have encoded 156 bits of data into a pack of 52 cards (exactly 3 bits per card). We have encoded the following part of the key: "04 f2 e1 38 24 4a 53 3d a8 0d 9b 34 7c 71 26 29 84 38 51"

Previous page    Next page